Understanding Procedural Generation
What is a grid
The grid is made up of tile objects, and each tile object represents a piece of generated terrain.
By lowering the tile size the resolution or quality of the procedurally generated world will go up, however load time at startup will also go up.
What is a Map Function:
Form
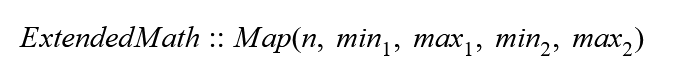
Inputs
* _n_ : the value to convert
* _min₁_ : lowest value of first range
* _max₁_ : highest value of first range
* _min₂_ : lowest value of the second range
* _max₂_ : highest value of the second range
Output
returns n converted to the second range
Description
Although not a part of the noise extension, the map function is very important. Allowing for an easy conversion between different ranges of numbers. For example, a noise function returns a value between -1 and 1, however you want the noise value to represent the opacity of an object which is between 0 and 255. Instead of doing the math to figure out how to convert -1-1 to 0-255 the map function will handle that for you.
Whatever range n is measured on becomes the first range and whatever range you want it measured on becomes your second range. So min1 becomes -1 since it's the minimum value for the first range and max1 becomes 1 since it's the maximum value for the first range. The same logic applies to the second range, min2 becomes 0 and max2 becomes 255.
So if the noise function returned 0 the map function would convert it to 127.5. If the noise function returned 0.1 the map function would convert it to 25.5.
What is Noise
Noise and random functions have a lot in common so the easiest way to understand noise is to look at the differences between the two.
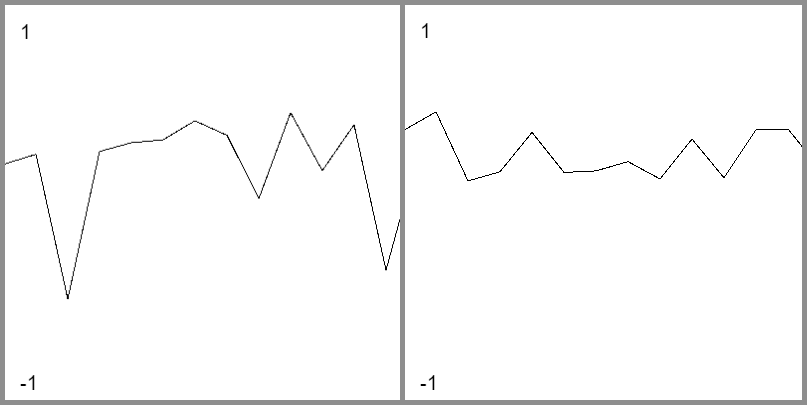The graph on the left shows a random number being placed between -1 and 1. On the right is a graph using noise to generate the values. Notice how the noise values smoothly change from the high points to the low points, unlike the random function where one value could be high and the next very low leading to a very uneven transition. This is the benefit of noise functions: they can create random, but consistent looking results.
What is the difference between Perlin and simplex noise
Perlin noise was invented by Ken Perlin in 1983 when he was working on the movie Tron to create more realistic looking textures. He would later win an Academy Award for his work on that film. Perlin created a simple algorithm that could create natural looking textures relatively quickly. Notably, Perlin never patented his algorithm which means that anyone can use his algorithm without risk of copyright infringement.
Simplex noise was also invented by Ken Perlin in 2001. He made this new noise algorithm to address some of the problems with Perlin noise like artifacts and slowness. However Ken Perlin patented his new creation meaning others could not legally use simplex noise without permission. This led to the open source community creating open-simplex noise. A freely available version of simplex noise which is used in the noise extension.
When choosing between Perlin and simplex, it's recommended that you use simplex noise because it is faster and more efficient and leads to better looking results.
What is the Difference Between 2D and 3D Noise
Noise functions have two varieties, 2 dimensional and 3 dimensional.
In a 2D noise function the 2 dimensions are the x dimension and the y dimension. Use this function in top-down or side-view games. This is the variation to use in most situations and recommended for beginners.
In a 3D noise function the 3 dimensions are x, y and z. Since GDevelop 2D game engine it may seem a bit weird to have a 3D noise function. However, when faking 3D in GDevelop this function may be useful. Also, the third dimension can also be used to represent time instead of z. This variation is not recommended for beginners.
1D noise
To achieve 1D noise simply use a 2D noise function and set one of the dimensions to a constant value. For example noise::simplex2(Variable(x), 0.5), since the y parameter never changes only the x, the noise function will now return a 1 dimensional result.